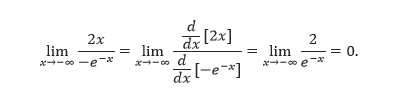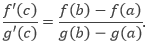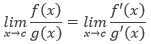Teknik Integral: Substitusi Trigonometri
Ada dua hal yang akan kita diskusikan dalam pembahasan ini. Pertama, kita akan mendiskusikan bagaimana penggunaan substitusi trigonometri dalam menyelesaikan permasalahan integral. Kedua, kita akan juga membahas penggunaan integral dalam memodelkan dan menyelesaikan permasalahan dalam kehidupan sehari-hari.
Substitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memuat bentuk akar

Tujuan dari penggunaan substitusi trigonometri adalah untuk menghilangkan akar tersebut dalam integran. Kita dapat melakukan hal ini dengan menggunakan identitas Pythagoras
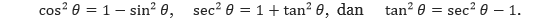
Sebagai contoh, jika a > 0, misalkan u = a sin θ, dengan –π/2 < θ < π/2. Maka

Perhatikan bahwa cos θ ≥ 0, karena –π/2 < θ < π/2.
Substitusi Trigonometri
- Untuk integral yang memuat √(a² – u²), misalkan u = a sin θ. Maka, didapatkan √(a² – u²) = a cos θ, di mana –π/2 < θ < π/2.

- Untuk integral yang memuat √(a² + u²), misalkan u = a tan θ.
Maka, √(a² + u²) = a sec θ, dengan –π/2 < θ < π/2.
- Untuk integral yang memuat √(u² – a²), misalkan u = a sec θ. Maka,


Catatan Batasan dari θ memastikan bahwa fungsi pada substitusi tersebut merupakan fungsi satu-satu. Faktanya, batasan tersebut merupakan interval yang sama di mana arcsinus, arctangen, dan arcsecan didefinisikan.
Integral Trigonometri
Pada pembahasan ini kita akan berlatih untuk menyelesaikan integral-integral yang memiliki bentuk
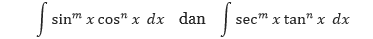
di mana m dan n adalah bilangan bulat positif. Untuk menemukan antiturunan dari bentuk-bentuk tersebut, pecahlah bentuk tersebut menjadi kombinasi dari integral trigonometri sedemikian sehingga kita dapat menggunakan Aturan Perpangkatan.
Sebagai contoh, kita dapat menyelesaikan integral berikut dengan memisalkan u = sin x. Sehingga, du = cos x dx dan diperoleh,
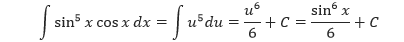
Untuk menyelesaikan integral-integral trigonometri, gunakan identitas-identitas berikut agar kita dapat menggunakan Aturan Perpangkatan.

Panduan untuk Menyelesaikan Integral yang Memuat Perpangkatan Sinus dan Cosinus
- Jika pangkat dari sinus adalah bilangan ganjil dan positif, simpan satu faktor sinus tersebut dan ubahlah faktor sisanya menjadi cosinus. Kemudian, ekspansi dan integralkan.
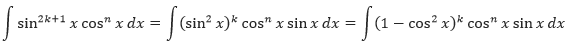
- Jika pangkat dari cosinus adalah bilangan ganjil dan positif, simpan satu faktor cosinus tersebut dan ubahlah faktor sisanya menjadi sinus. Kemudian, ekspansi dan integralkan.
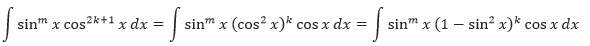
- Jika pangkat dari sinus dan cosinus keduanya genap dan tidak negatif, gunakan secara berulang identitas berikut,
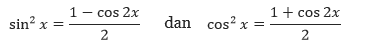
untuk mengubah integran menjadi perpangkatan ganjil dari cosinus. Kemudian lanjutkan sesuai panduan nomor 2.
Contoh 1: Pangkat dari Sinus Ganjil dan Positif
Tentukan,
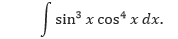
Pembahasan Karena kita berharap untuk menggunakan Aturan Perpangkatan dengan u= cos x, maka simpan satu faktor sinus untuk membentuk du dan ubah faktor-faktor sinus sisanya menjadi cosinus.
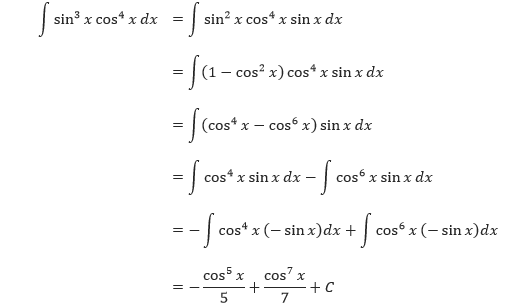
Pada Contoh 1 di atas, pangkat m dan n keduanya merupakan bilangan bulat positif. Bagaimanapun, teknik yang sama dapat digunakan selama salah satu dari m atau nmerupakan bilangan ganjil dan positif. Sebagai contoh, pada contoh selanjutnya pangkat dari cosinusnya 3, sedangkan pangkat dari sinusnya –1/2.
Contoh 2: Pangkat dari Cosinus Ganjil dan Positif
Tentukan,
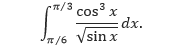
Pembahasan Karena kita akan menggunakan Aturan Perpangkatan dengan u = sin x, maka simpan satu faktor cosinus untuk membentuk du dan ubah faktor-faktor cosinus sisanya menjadi sinus.
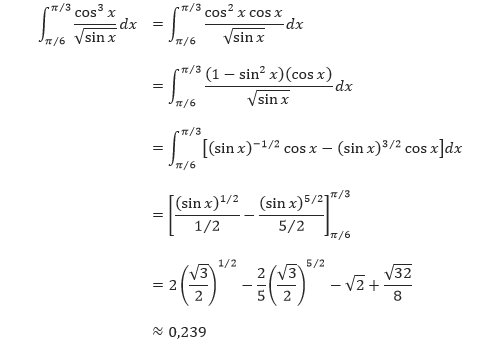
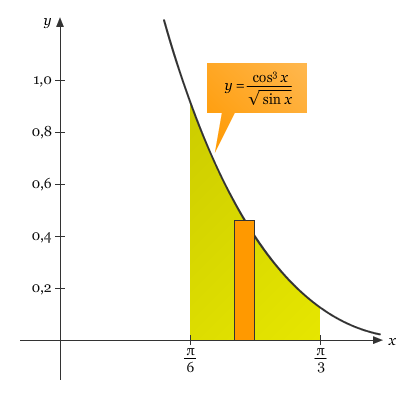
Gambar di bawah ini menunjukkan daerah yang luasnya direpresentasikan oleh integral tersebut.
Pada pembahasan ini kita akan berlatih menemukan antiturunan dengan menggunakan integral parsial. Selain itu, di bagian akhir pembahasan ini, kita juga akan menggunakan metode tabulasi dalam melakukan proses integral parsial tersebut. Teknik integral parsial dapat diterapkan dalam berbagai macam fungsi, dan secara khusus teknik tersebut sangat berguna ketika dijumpai integran yang melibatkan perkalian fungsi-fungsi aljabar dan transendental. Sebagai contoh, integral parsial akan sangat berfungsi dengan baik untuk menyelesaikan,

Integral parsial didasarkan pada rumus turunan dari perkalian dua fungsi.
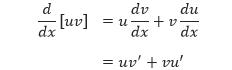
di mana u dan v adalah fungsi-fungsi yang terdiferensialkan dalam x. Jika u’ dan v’ kontinu, kita dapat mengintegralkan kedua ruas dari persamaan di atas dan memperoleh
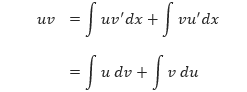
Dengan menulis kembali persamaan di atas, diperoleh teorema berikut.
Teorema 1: Integral ParsialJika u dan v adalah fungsi-fungsi dalam x yang kontinu dan terdiferensialkan, maka
Rumus integral parsial ini menyatakan integral aslinya ke dalam bentuk integral yang lain. Berdasarkan pemilihan u dan dv, akan lebih mudah menyelesaikan bentuk integral yang kedua daripada bentuk aslinya. Karena pemilihan u dan dv sangatlah krusial dalam proses integral parsial, berikut ini panduan dalam memilih u dan dv.
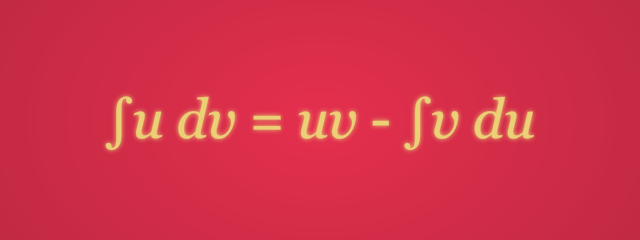
Panduan dalam Proses Integral Parsial
- Cobalah untuk memisalkan dv sebagai bagian yang sangat rumit dari integran yang sesuai dengan aturan dasar integral. Sehingga u merupakan faktor lainnya dari integran.
- Cobalah untuk memisalkan u sebagai bagian dari integran yang turunannya lebih sederhana dari u. Selanjutnya dv merupakan faktor integral lainnya.
Perhatikan bahwa dv selalu memuat dx dari integran aslinya.
Untuk lebih memahami bagaimana menyelesaikan permasalahan integral dengan menggunakan metode integral parsial, perhatikan beberapa contoh berikut.
Contoh 1: Integral Parsial
Tentukan,
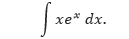
Pembahasan Untuk menerapkan integral parsial, kita perlu untuk menuliskan integral tersebut ke dalam

Terdapat beberapa cara untuk melakukan hal tersebut, yaitu

Panduan dalam pemilihan u dan dv sebelumnya menyarankan kita untuk memilih pilihan pertama karena turunan dari u = x lebih sederhana dari x, dan dv = ex merupakan bagian yang paling rumit dari integran yang sesuai dengan aturan dasar integral.
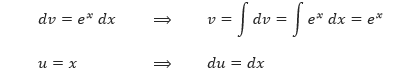
Sekarang, dengan integral parsial akan dihasilkan

Untuk memeriksa hasil pengintegralan ini, kita dapat menurunkan hasil tersebut untuk mendapatkan integran aslinya.
Catatan Pada contoh 1 di atas kita tidak perlu menuliskan konstanta ketika menyelesaikan
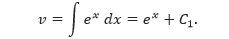
Untuk mengilustrasikan hal ini, cobalah mengganti v = ex dengan v = ex + C1 kemudian terapkan proses integral parsial untuk melihat bahwa kamu akan mendapatkan hasil yang sama.
Aturan L’Hôpital
Aturan L’Hôpital menyatakan bahwa dalam kondisi tertentu, limit dari pembagianf(x)/g(x) dapat ditentukan dengan menggunakan limit pembagian dari turunan-turunannya, yaitu
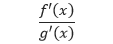
Untuk membuktikan teorema ini, digunakan Teorema Nilai Rata-rata yang Diperluas, seperti berikut.
TEOREMA NILAI RATA-RATA YANG DIPERLUASJika f dan g memiliki turunan pada interval terbuka (a, b) dan kontinu pada [a, b] sedemikian sehingga g’(x) ≠ 0 untuk setiap x di dalam (a, b), maka ada titik c di (a, b) sedemikian sehingga,
Bukti Kita dapat menganggap bahwa g(a) ≠ g(b), karena jika tidak, menurut Teorema Rolle, akan mengakibatkan g’(x) = 0 untuk suatu x di (a, b). Sekarang, didefinisikan h(x) sebagai berikut.
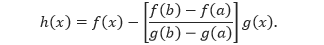
Maka
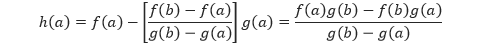
dan
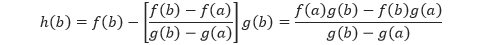
dan dengan menggunakan Teorema Rolle, ada titik c di (a, b) sedemikian sehingga
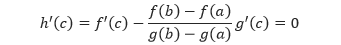
yang menyebabkan bahwa,
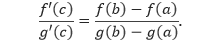
Setelah membuktikan Teorema Nilai Rata-rata yang Diperluas, sekarang perhatikan Teorema L’Hôpital berikut.
ATURAN L’HÔPITALMisalkan f dan g adalah fungsi-fungsi yang memiliki turunan pada interval terbuka (a, b) yang memuat c, kecual pada c itu sendiri. Anggap g(x) ≠ 0 untuk setiap x di (a, b), kecuali pada c itu sendiri. Jika limit dari f(x)/g(x) untuk x mendekati c menghasilkan bentuk tidak tentu 0/0, maka
apabila limit di ruas kanan ada (atau tak hingga). Hasil ini juga dapat diterapkan jika limit f(x)/g(x) untuk x mendekati c menghasilkan bentuk-bentuk tak tentu ∞/∞, (–∞)/∞, ∞/(–∞), dan (–∞)/(–∞).
Seperti yang telah disinggung sebelumnya, Aturan L’Hôpital tersebut akan dibuktikan dengan menggunakan Teorema Nilai Rata-rata yang Diperluas. Karena banyak kasus dalam aturan ini, maka pada pembahasan ini hanya akan dibuktikan untuk satu kasus saja. Untuk kasus yang lain diserahkan kepada pembaca sebagai latihan.
Bukti Perhatikan satu kasus untuk,

Selanjutnya definisikan fungsi baru sebagai berikut.

Untuk setiap x, c < x < b, F dan G memiliki turunan pada (c, b] dan kontinu pada [c, b]. Sehingga, Teorema Nilai Rata-rata yang Diperluas dapat diterapkan untuk menyimpulkan bahwa ada bilangan z di (c, x) sedemikian sehingga
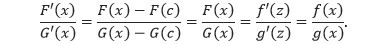
Akhirnya, dengan memisalkan x mendekati c dari kanan, x → c+, didapatkan z → c+karena c < z < x, dan
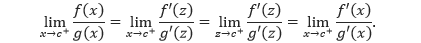
Catatan Kesalahan kadang-kadang dilakukan dengan menggunakan Aturan Turunan pada Pembagian f(x)/g(x) dalam menerapkan Aturan L’Hôpital ini. Pastikan bahwa aturan ini memuat f ’(x)/g’(x), bukan turunan dari f(x)/g(x). Selanjutnya perhatikan beberapa contoh berikut.
Contoh 1: Bentuk Tak Tentu 0/0
Tentukan nilai limit dari (e2x – 1)/x untuk x mendekati 0.
Pembahasan Karena dengan menggunakan substitusi langsung menghasilkan bentuk tak tentu 0/0,
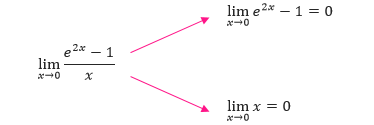
sehingga dapat diterapkan Aturan L’Hôpital, seperti yang ditunjukkan di bawah ini.
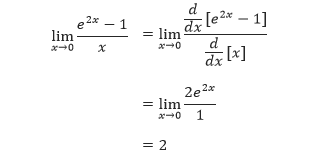
Contoh 2: Penerapan Aturan L’Hôpital Lebih dari Satu Kali
Tentukan limit x2/e–x untuk x mendekati negatif tak hingga.
Pembahasan Karena dengan substitusi langsung akan menghasilkan bentuk tak tentu ∞/∞, maka gunakan Aturan L’Hôpital.
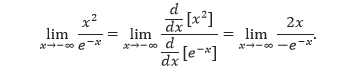
Limit ini masih menghasilkan bentuk tak tentu (–∞)/(–∞), sehingga Aturan L’Hôpital dapat diterapkan kembali.